The output response of any intact oscillatory system subjected to a Gaussian excitation is also Gaussian in nature. On the contrary, when the system contains any type of underlying nonlinearity, the output signal is definitely non-Gaussian. In beam structures, the presence of fatigue-breathing cracks significantly influences the dynamic response characteristics under Gaussian excitation. The presence of such cracks alters the response to be nonlinear, and the non-Gaussianity of the system will arise. In order to examine the non-Gaussianity features and ability for the detection and localization of fatigue cracks, several breathing crack identification scenarios in beam-like structures are presented in this paper. The effects of single and multiple breathing cracks corresponding to different boundary conditions on the responses of beams are studied. The results are analyzed based on the higher-order time-domain transformations. Higher-order transformations, namely the skewness and kurtosis coefficients in addition to the Shannon entropy, are exploited to provide dynamic details about the response, which the conventional second-order statistics cannot show. The results exhibit that the proposed methods are robust and immune to noise and can detect and localize breathing cracks with different sensitivities.

Single Breathing Crack

1. Case Study 1

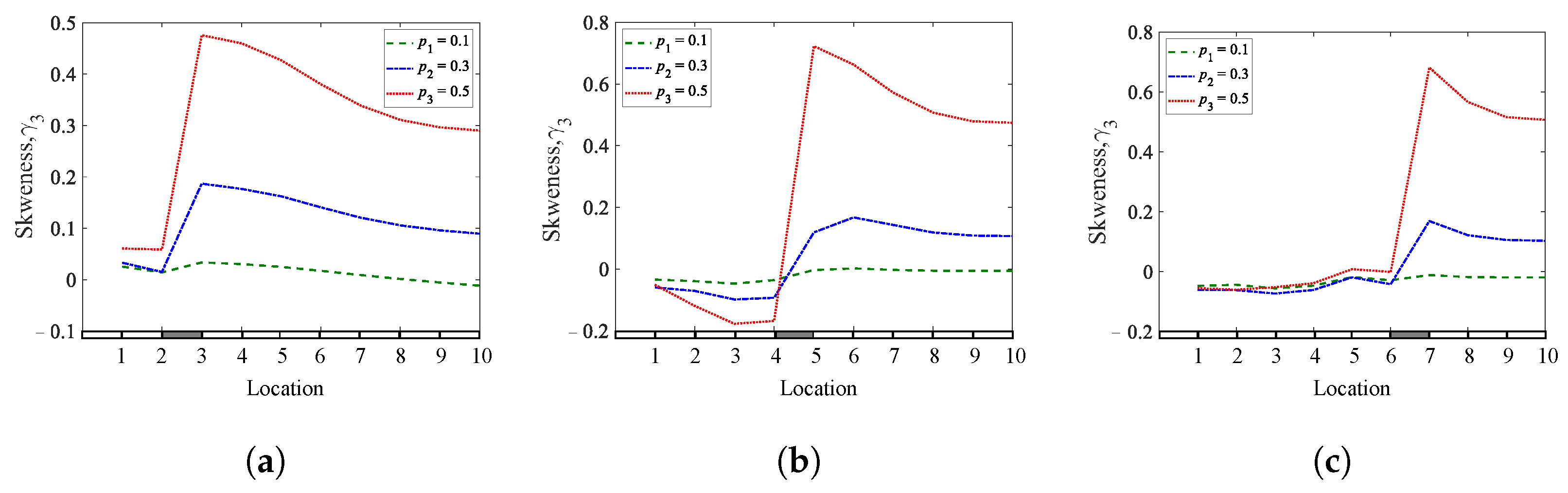
Figure 1. Skewness coefficients of a cantilever beam for different crack depths and locations: (a)q₁= 0.25; (b)q₂= 0.45; (c) q₃ = 0.65.

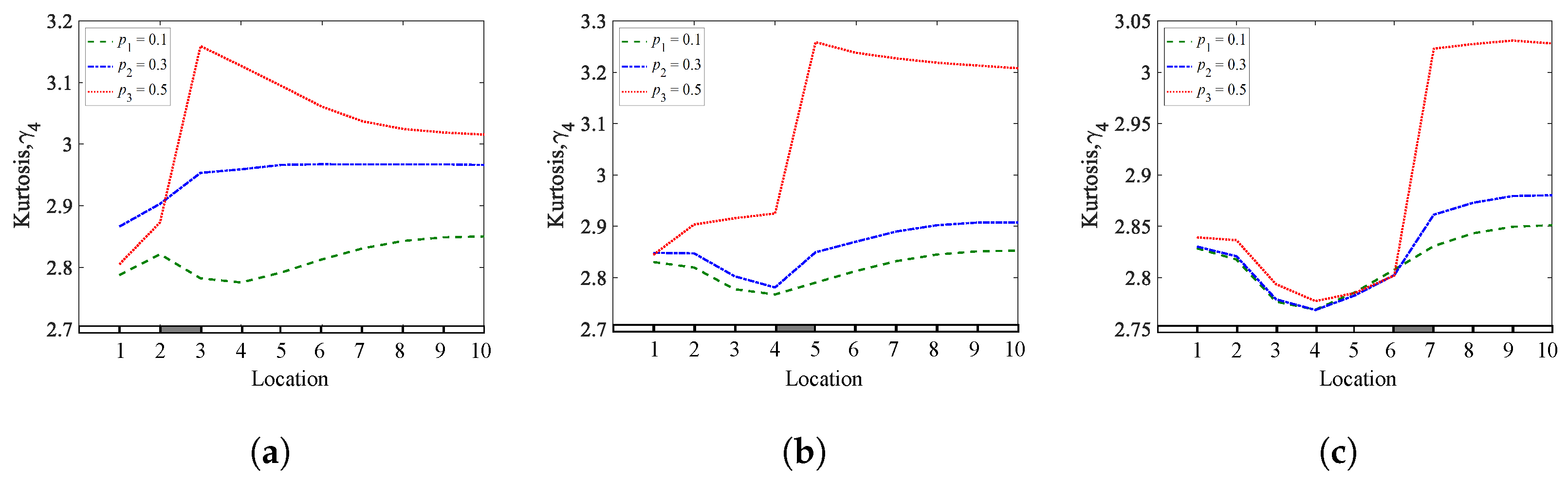
Figure 2. Kurtosis coefficients of a cantilever beam for different crack depths and locations: (a)q₁= 0.25; (b)q₂= 0.45; (c) q₃ = 0.65.

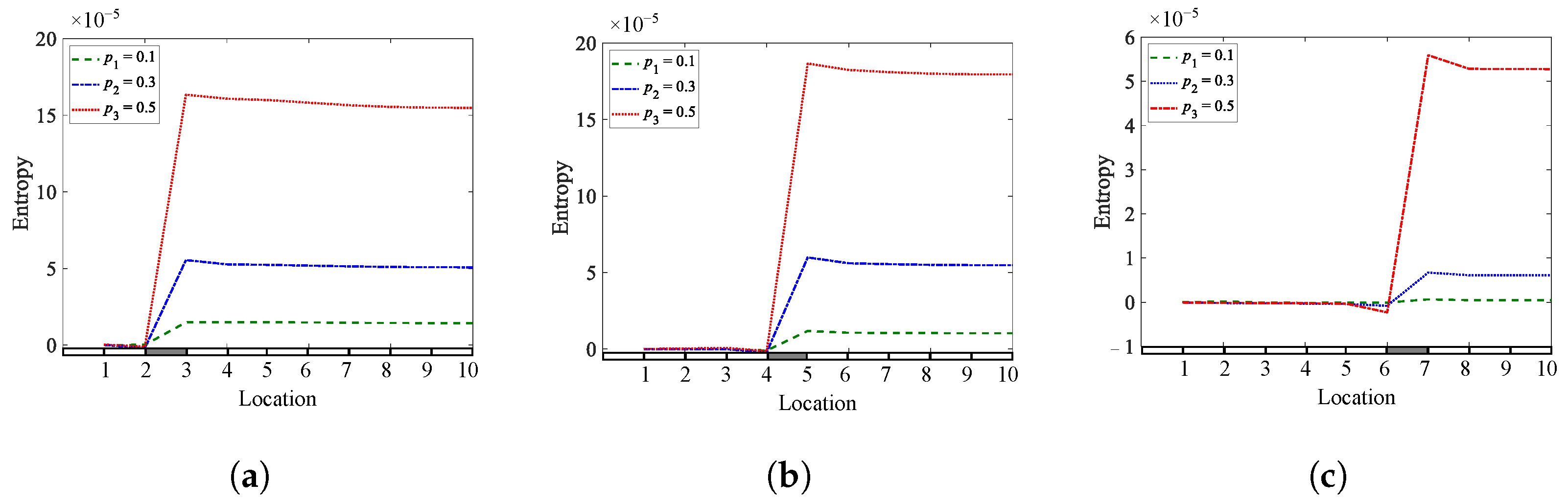
Figure 3. Entropy of a cantilever beam for different crack depths and locations: (a)q₁= 0.25; (b)q₂= 0.45; (c) q₃ = 0.65.

2. Case Study 2

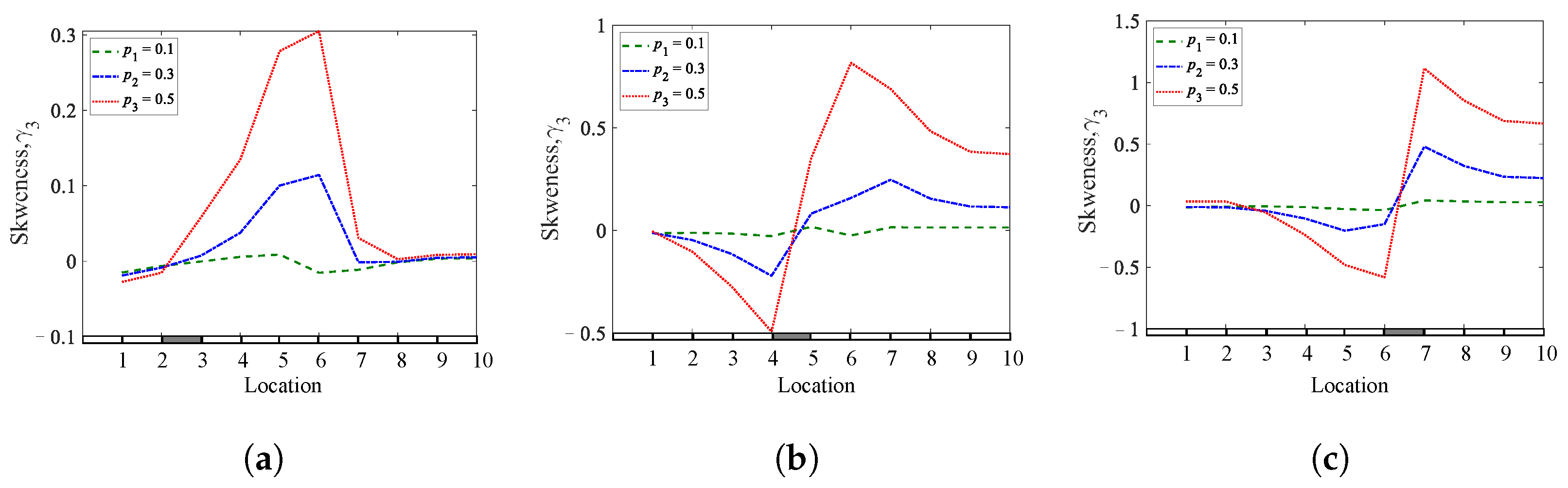
Figure 4. Skewness coefficients of a cantilever, simply supported beam for different crack depths and locations:  (a)q₁= 0.25; (b)q₂= 0.45; (c) q₃ = 0.65.

Figure 5. Kurtosis coefficients of a cantilever, simply supported beam for different crack depths and locations:  (a)q₁= 0.25; (b)q₂= 0.45; (c) q₃ = 0.65.

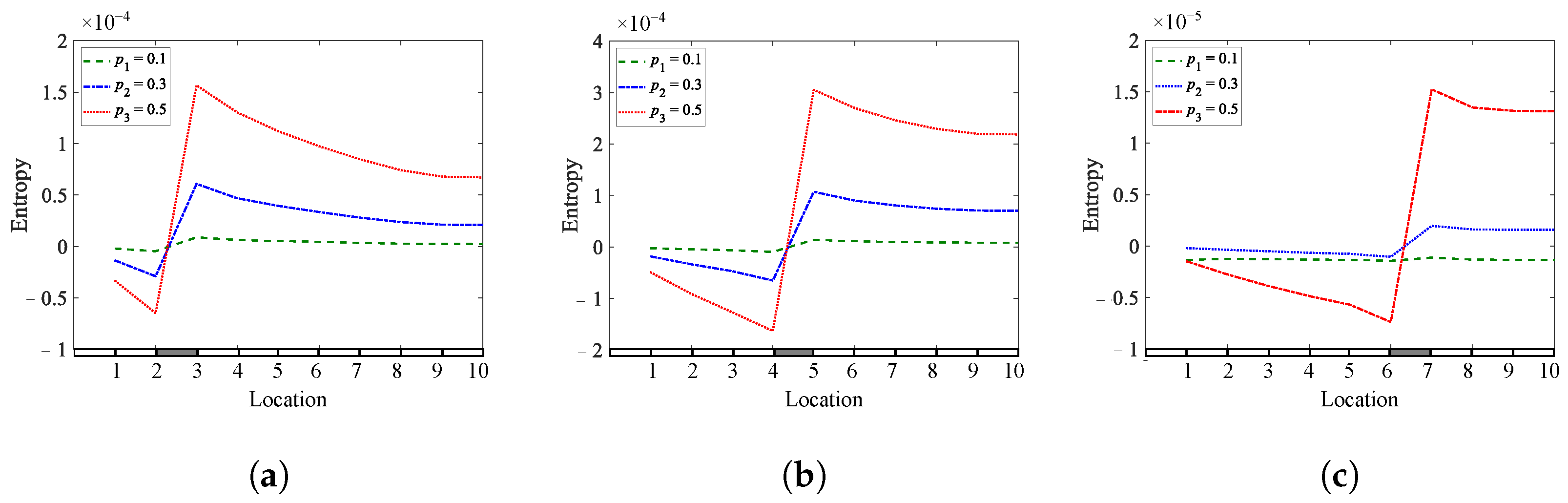
Figure 6. Entropy of a cantilever, simply supported beam for different crack depths and locations:  (a)q₁= 0.25; (b)q₂= 0.45; (c) q₃ = 0.65.

3. Case Study 3

Figure 7. Skewness coefficients of a fixed-fixed beam for different crack depths and locations: (a)q₁= 0.25; (b)q₂= 0.45; (c) q₃ = 0.65.

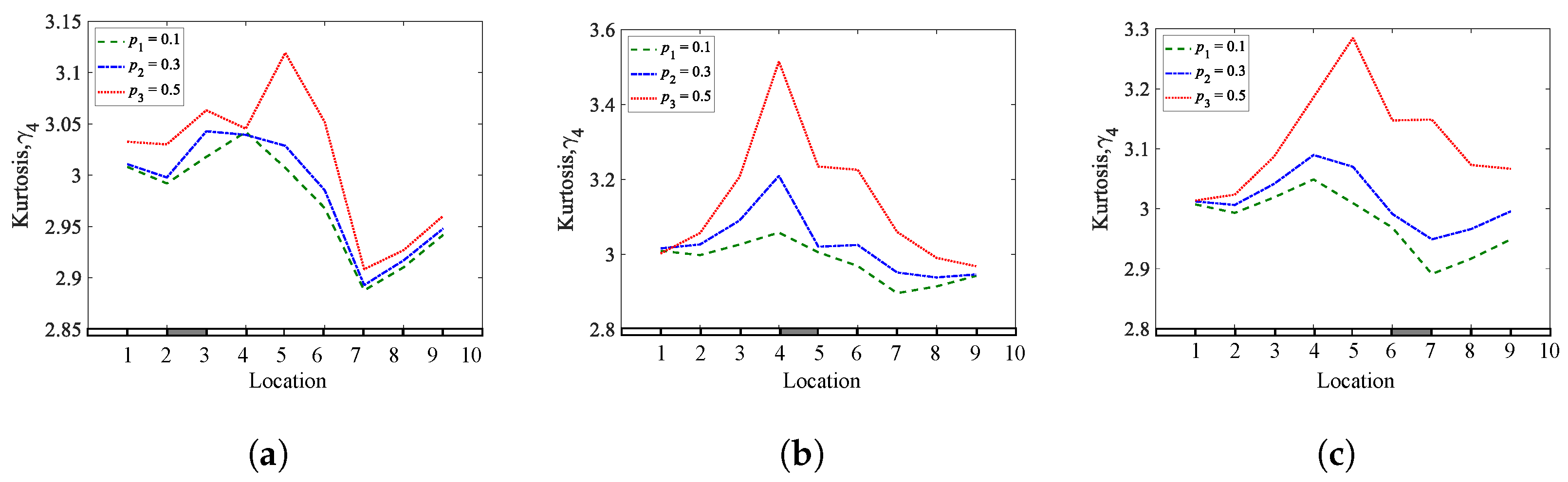
Figure 8. Kurtosis coefficients of a fixed-fixed beam for different crack depths and locations: (a)q₁= 0.25; (b)q₂= 0.45; (c) q₃ = 0.65.

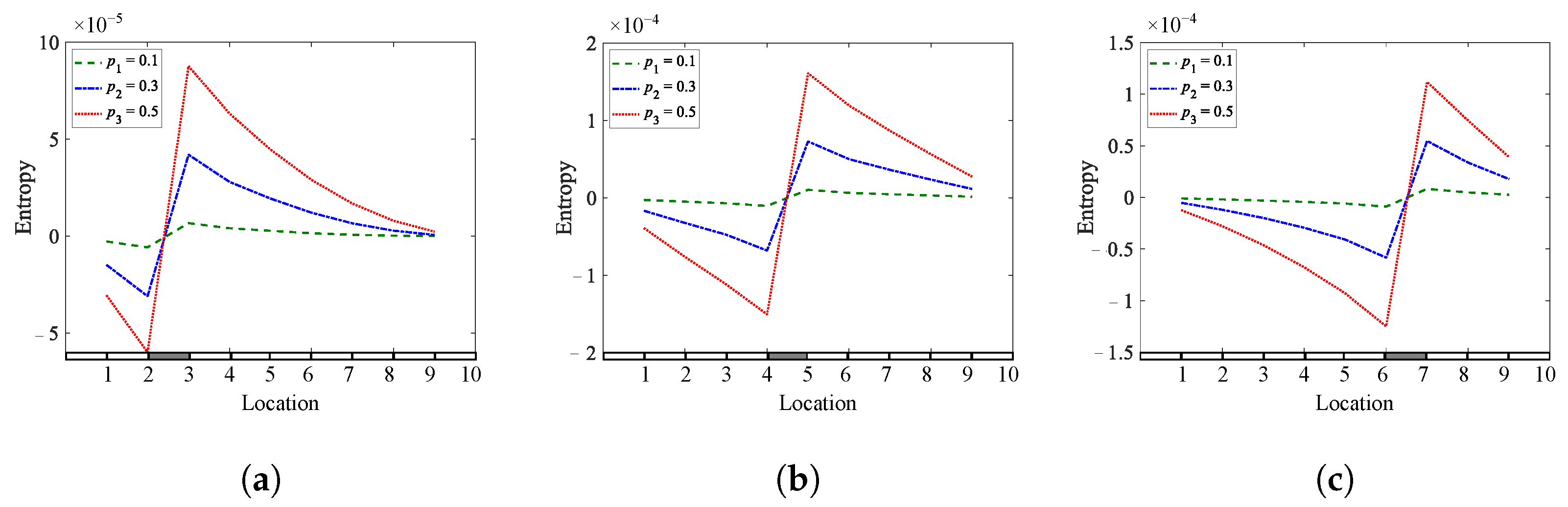
Figure 9. Entropy of a fixed-fixed beam for different crack depths and locations: (a)q₁= 0.25; (b)q₂= 0.45; (c) q₃ = 0.65.

4. Case Study 4

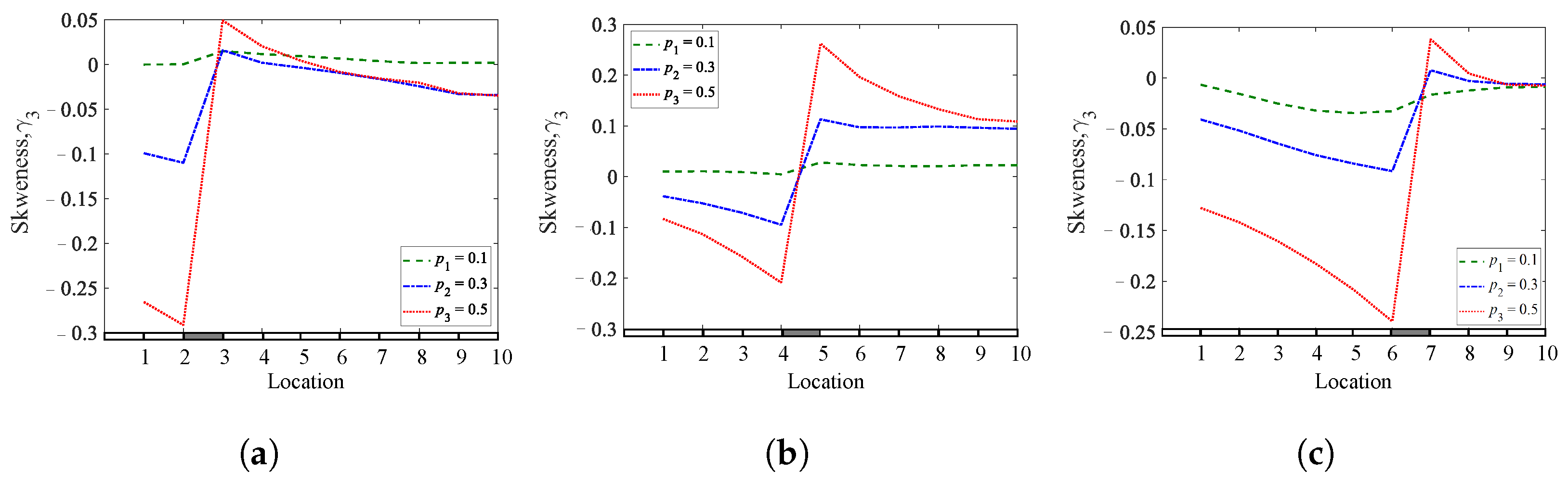
Figure 10. Skewness coefficients of a simply supported beam for different crack depths and locations: (a)q₁= 0.25; (b)q₂= 0.45; (c) q₃ = 0.65.

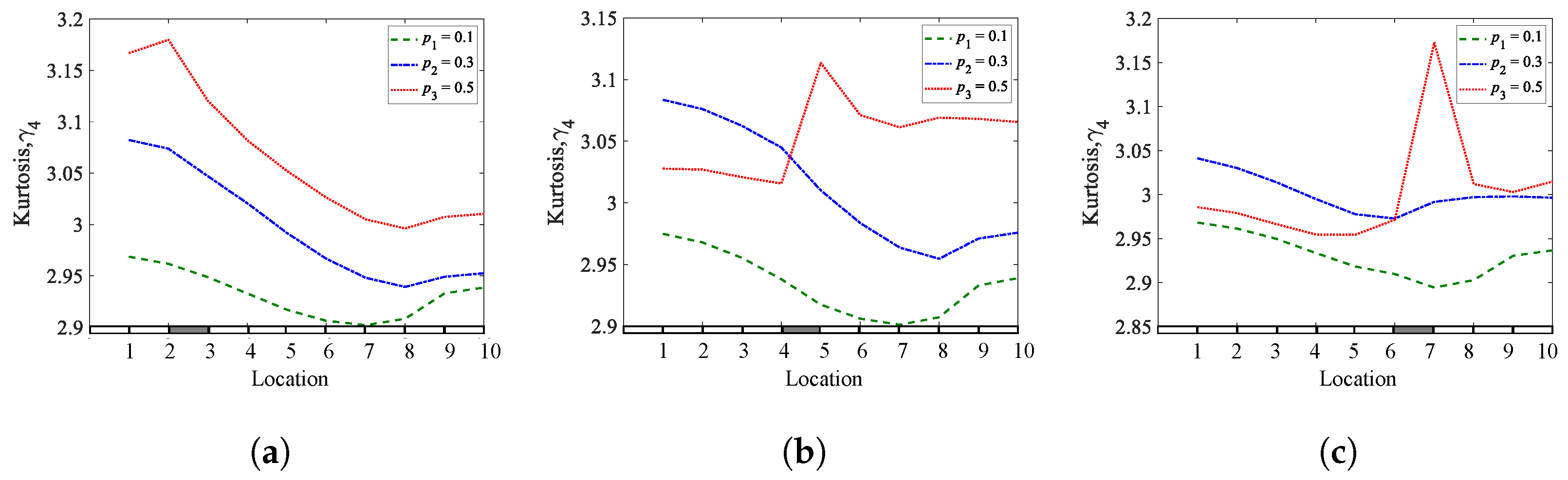
Figure 11. Kurtosis coefficients of a simply supported beam for different crack depths and locations: (a)q₁= 0.25; (b)q₂= 0.45; (c) q₃ = 0.65.

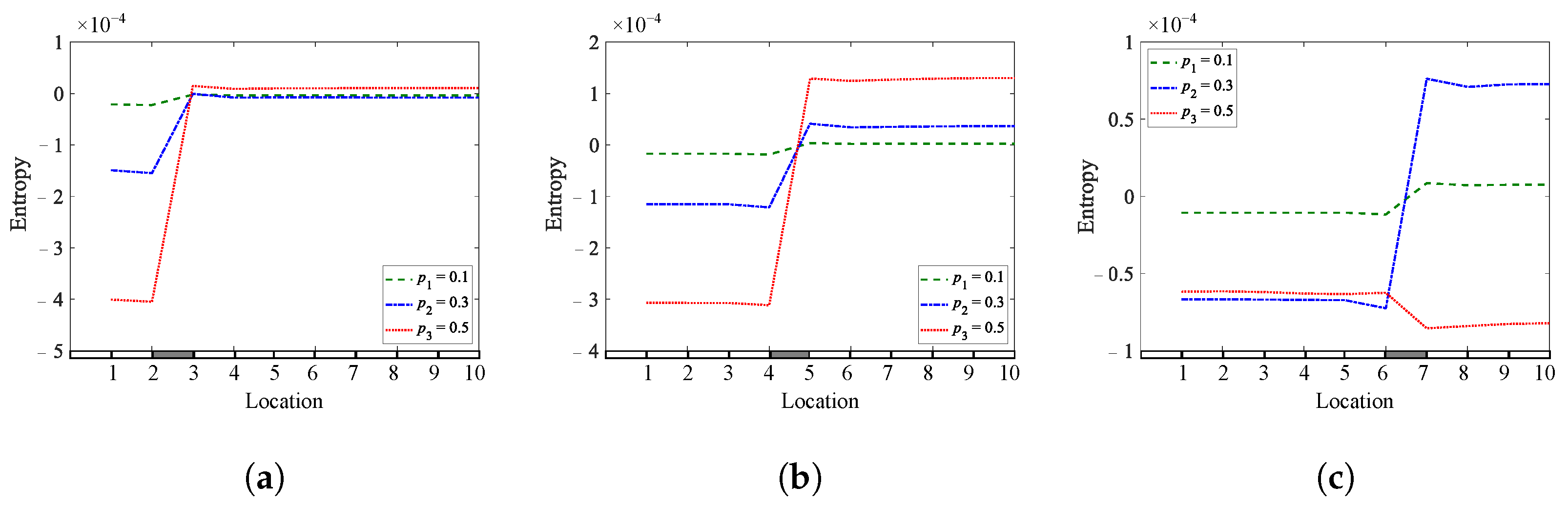
Figure 12. Entropy of a simply supported beam for different crack depths and locations: (a)q₁= 0.25; (b)q₂= 0.45; (c) q₃ = 0.65.

DOI: 10.3390/MATH10111853